|
|
| |
수나사의 나사산과 암나사의 나사홈이 서로 맞물리는 높이와 기준 나사산형의 높이와의 비율을
걸림률이라고 한다. 즉, 볼트의 나사산과 너트의 나사산이 서로 물려있는 양을 비율로 표시한 것이다. 이것을 식으로 표현 하면 아래와 같다.
|
|
|
(수나사 외경 - 암나사 내경) |
|
|
걸림률(%)= |
|
x 100 |
|
|
2 x 숫나사산의 기준높이 |
| |
|
이 걸림률은 여러 가지 의미를 갖고 있다. 걸림률이 크다면 나사산 끼리의 결합이 강하게 되어 있어
더 큰 힘으로 조일 수 있으나 조임 작업에 많은 힘이 들어 가게 된다. 반대로 걸림률이 작다면 결합 및 해체가 쉬운 반면 큰힘을 지지하기 어렵다. 따라서, 일반적으로 큰 힘이 걸리지 않는 경우는 걸림률을 작게 하는 등 나사의 선택이나, 탭구멍을 설계할 시에 반드시 고려해야 하는 중요한 요소중의 하나이다. | |
| |
|
| |
| 수나사의 크기가 정해져있는 상황에서 결합모재에 나사구멍을준비할경우 |
| |
| |
나사산의 강도는 나사산의 단면적에 비례하게 된다. 걸림률에 따른 나사산의 단면적 변화를 보기 위해 수나사 호칭경(외경)은 일정하다고 가정하고 암나사의 내경을 변경하여 걸림률을 계산해 보았다.
| |
| |
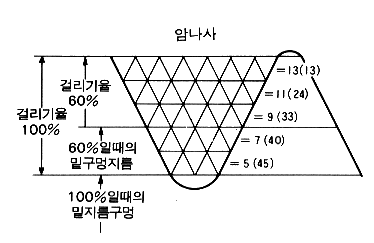 |
| ( 괄호안의 숫자는 누계합을 나타냄 ) | |
| |
나사산의 강도는 나사산의 단면적에 비례하게 된다. 걸림률에 따른 나사산의 단면적 변화를 보기 위해 수나사 호칭경(외경)은 일정하다고 가정하고 암나사의 내경을 변경하여 걸림률을 계산해 보았다.
|
상기 그림에서와 같이 암나사산의 단면적을 작은 삼각형(45개)으로 분할했다.
만일 걸림률을 60%로 가정한다면, 암나사의 나사산의 면적은 33개의 작은 삼각형이므로73.3%(33/45x100)가 된다. 걸림률을 80%로 가정하면 암나사의 나사산의 면적은 40개의
작은 삼각형이므로 89%(40/45x100)가 된다 상기 결과를 보면, 걸림률이 작아지는 것에 비하면
단면적의 줄어듬은 작은 편임을 알 수 있다. 암나사의 경우 내경에 해당하는 구멍을 드릴작업을 통해
가공한 다음 탭으로서 나사산 부위를 만들게 된다. 이렇게 내경에 해당하는 구멍을 밑구멍이라고 하며 밑구멍의 지름값을 결정하는 것이 물림률을 결정하게 되는 것이다. |
밑구멍지름
(암나사 내경) |
|
|
|
걸림률 (%) |
| = |
호칭경 - 2 x (0.541266 x 피치 ) |
x |
|
|
|
|
100 | | |
밑구멍의 지름은 가능한 크게 하여 탭으로 절삭해 내는 양을 최소화하는 것이 탭에 걸리는 절삭 부하도 적어 가공이 용이하고 공구의 수명도 길어진다.
예) 호칭경이 M10x1.5 이고 h7의 공차를 갖는 나사를 60%의 걸림율을 채택한다면
수나사 외경의 최대값 = 10.0
밑구멍 지름 = 10.0 - (2*0.541266*1.5*60/100) = 9.026
수나사 외경의 최소값 = 9.985
밑구멍 지름 = 9.985 - (2*0.541266*1.5*60/100) = 9.011 상기 결과에서 h7의 공차값인 0.015의 차이는 걸림률로는 0.9% 정도의 차이가 나게 된다.
따라서 밑구멍을 설계할 때는 공차를 무시하고 호칭경으로 계산해도 무리가 없다.
(본 예는 절삭탭에 의한 가공에 적용되며 전조 가공을 하는 무절삭탭-무홈탭이라고도 함-에 의한
경우는 적용되지 않음) | |